Polarization-optical characteristics of light in one-dimensional photonic crystals with a twisted nematic defect layer
The great technological breakthrough of display industry (since 1970 till now) has come true thanks to the electrically switchable transmission layer of liquid crystals (LCs) with a helical optical axis. Such a twisted LC layer is called the twist cell. The twist-cell placed into an optical resonator shows some new subtle effects, which have been the subject of investigations conducted at our laboratory in 2010-2014. The first effect is avoided crossing of optical mode frequencies. The second effect is the geometric phase of twist, a classical analogue of the spin-orbit interaction.
The polarization of the transmitted light rotates around the optical axis due to the Maugin waveguide mode. In order to measure the phase shift, the system is placed into a Fabry–Perot optical resonator. Spectral transmission peaks are formed at whole number N of wave periods per resonator cycle 2L:
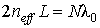 (1)
(1)
where λ0 – is the wavelength in vacuum and neff – is the effective refraction index (RI). However, the measurements are complicated by the anisotropic medium of the resonator generating two sets of peaks with polarizations along the main axes of the permittivity tensor and different effective RIs (neff, n'eff). Rotation of the main axes makes resonant polarizations elliptical, results in mode coupling upon reflection from mirrors, and is manifested as coupling between normal optical modes (avoided crossing).
In [1], defect modes were investigated in a band gap of an electrically tunable 1D photonic crystal infiltrated with a twisted-nematic liquid crystal. Their frequency shift and interference under applied voltage were studied both experimentally and theoretically. We deal with the case when the defect layer thickness is much larger than the wavelength (i.e., the Mauguin condition). It was shown theoretically that the defect modes could have a complex structure with the elliptic polarization. Two series of polarized modes are coupled with each other and exhibit an avoided crossing phenomenon in the case of opposite parity.
Fig.6_1. Calculated transmission spectrum of unpolarized light versus voltage.
Defective modes have rotating polarization with an ellipse oriented along the LC director (L-mode) or transverse (T-mode). Figure 6_1 shows the calculated transmission spectrum of unpolarized light versus voltage. Darker color corresponds to higher transmittance. The regions of intersection of T-mode No. 68 with L-modes No. 74 (a), 72 (c), and 70 (e) are shown by dashed circles (the same mode parity). The regions of coupling of T-mode No. 68 with L-modes No. 73 (b), 71 (d), and 69 (f) are shown by solid circles (opposite mode parity). Dashed lines separate four voltage ranges with different behaviors of the mode:
- 0 < U < UC = 0.78 V. There is no dynamics below the Fréedericksz threshold.
- 0.78 V < U < 1.1 V. The L-mode peak series moves quickly toward shorter wavelengths, but the T-mode peak series remains virtually at fixed wavelengths due to the Mauguin condition ensuring the effective ordinary refractive index (Fig. 1a).
- 1.1 V < U < 2.0 V. The Mauguin condition breaks down in the thin middle layer (Fig. 1b). LC in this layer exhibits a steep azimuthal rotation and low effective birefringence Dneff << n. T-modes are coupled with L-modes of opposite parity (see the text further down).
- 2.0 V < U. Now, the voltage is approximately three times higher than the Fréedericksz threshold. The middle LC layer has a virtually homeotropic director orientation (Fig. 1c). The LC layers on the borders are in-plane-oriented and there is no twist and no Mauguin rotation of polarization. The L- and T-modes become linearly polarized. The vertical and horizontal directions without clockwise or counterclockwise twist become symmetric. Peaks of L- and T-modes with the same mode number combine to form doublets. These doublets experience a voltage-induced blueshift as the integral refractive index goes down with LC boundary layers thinning-down.
In [2], new anisotropic mirrors were proposed for decoupling of the elliptically polarized eigenmodes in an anisotropic optical cavity. It was shown that twisting makes the effective RI less than the ordinary RI or greater than the extraordinary RI ne. (neff <n0 < ne <n'eff).
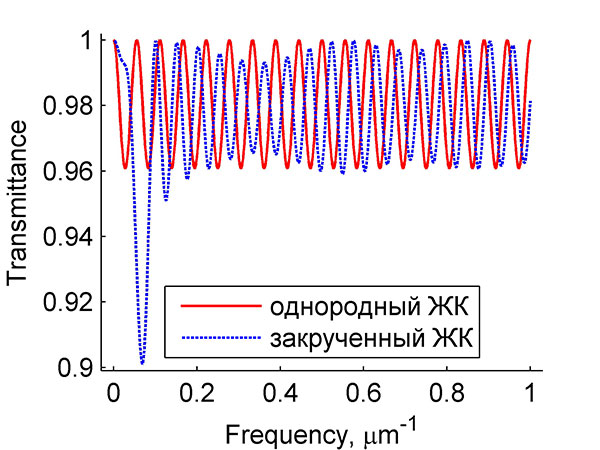
Fig. 6_2. Transmittance spectra of the transverse mode in an anisotropic resonator.
Figure 6_2 shows transmittance spectra of the transverse mode in an anisotropic resonator. We considered the cases when there was no twisting and there was twisting through 180 degrees. The spectra were computed using the Berreman method, which generalizes the transfer matrix approach to anisotropic media. Normalized RI no = 0.9, ne = 1.1 were used in our computations; the resonator length was 10 μm. The twisted structure exhibits low transmittance at a frequency of ~0.1 μm–1 corresponding to a wavelength of 10 μm, due to the reflection of light from the structure in the photonic band gap.
It can be seen that twisting shifts the peaks to the short-wavelength region. At the same time, the displacement is greater at lower frequencies. The shortwave shift reflects the decrement in effective RI (1), which becomes lower than the ordinary RI.
The discussed phenomenon suggests a sort of potential for application as a light valve, monochromatic selector, etc. In addition to the above-mentioned spectral and electro-optical applications, the high-precision method that has been utilized in this study can also provide an alternative way for obtaining the LC elastic constants through simulation of the inverse problem.
- I. V. Timofeev, Y.-T. Lin, V. A. Gunyakov, S. A. Myslivets, V. G. Arkhipkin, S. Ya. Vetrov, W. Lee, and V. Ya. Zyryanov, Phys. Rev. E 85, 011705 (2012).
- I. V. Timofeev and S. Y. Vetrov, Spectral manifestation of an effective refraction index in a chiral optical medium inside a Fabry –Perot resonator with anisotropic mirrors, Bull. Russ. Acad. Sci. Phys. 78, 1599 (2014).
